Introduzione al Missile Balistico

In questo articolo si analizzeranno gli aspetti principali nell’ingegnerizzazione di un missile balistico. In particolare, si evidenzieranno i fondamenti fisici, accompagnati dalla loro descrizione in termini matematici (quando possibile); verranno inoltre rimarcati gli aspetti critici nella progettazione. L’obiettivo dell’articolo è quello di far comprendere ciò che c’è dietro alla progettazione di un sistema complesso.

In primo luogo, per missile balistico si intende un missile che presenta, appunto, una traiettoria balistica, esattamente come quella di un proiettile di un’arma da fuoco o di un grave lanciato in una precisa direzione; il missile balistico ha lo scopo di portare un certo carico (payload), consistente di una testata convenzionale o nucleare ad una precisa distanza (range)

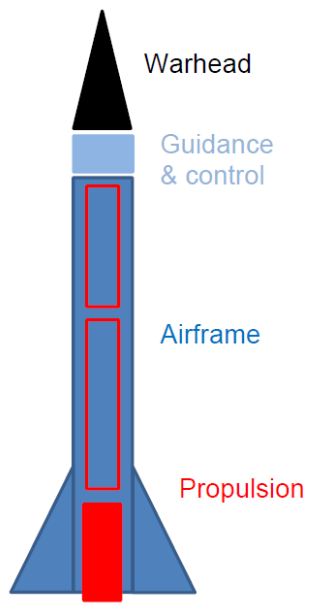
Dal punto di vista ingegneristico, un missile è un sistema complesso ma può essere facilmente schematizzato in pochi sottosistemi:

L’attenzione verrà concentrata solo sui seguenti aspetti che risultano essere di fondamentale importanza nella progettazione:

• Traiettoria (fasi di volo, angolo e velocità di burn-out, range)
• Propulsione (spinta, GNC)
• Rientro ed Accuratezza

Traiettoria

Le fasi di volo di un missile balistico sono ben delineate, sebbene dipendano dal numero di stages presenti ma, prescindendo dal loro numero, le fasi rientrano nelle seguenti tre:

• Boost Phase: è la fase che va dal lancio fino al burn-out, ovvero allo spegnimento del motore. In questa fase, che dura pochi minuti, avviene l’accelerazione del missile fino alla velocità di burn-out. Questa fase è essenziale per la definizione del range, quindi del raggio d’azione.
• Midcourse Phase: è la fase in cui il missile segue una traiettoria balistica e dove la resistenza atmosferica è trascurabile. Nel caso di missili balistici a lungo raggio può durare decine di minuti.
• Re-entry Phase: è qui che avviene il rientro della testata del missile e gli effetti atmosferici sono importantissimi, sia dal punto di vista delle sollecitazioni sulla struttura che in termini di accuratezza.

Perché la resistenza atmosferica è trascurabile nella Midcourse Phase?

Il missile, così come un’ala di un velivolo, è un oggetto immerso in un fluido (aria) che ne ostacola il moto; nella nostra vita quotidiana, l’aria non esercita un’elevata resistenza sul nostro corpo mentre ci muoviamo, ma possiamo sperimentare, in una giornata molto ventosa, difficoltà a camminare. Comprendiamo, quindi, che l’effetto della resistenza dell’aria è tanto maggiore quanto la velocità di quest’ultima o quanto un oggetto viaggi velocemente in essa (del resto le due cose sono speculari).

La resistenza atmosferica $D$ può essere definita tramite una semplice equazione:

$$D = \frac{1}{2} \rho V^2 S_{ref} C_{D}$$

$\rho$ è la densità dell’aria, $V$ è la velocità dell’oggetto che sta viaggiando nel fluido, $S_{ref}$ è una superficie di riferimento (nel caso di un missile, considerato come un cilindro, corrisponde alla sua area di base $\pi r^2$), $C_D$ è il coefficiente di resistenza.

La precedente equazione ci mostra quindi che più grandi sono i termini a destra (nel secondo membro), maggiore è la resistenza. Ad esempio non c’è da meravigliarsi che più grande è l’oggetto ($S_{ref}$), più fatica fa l’oggetto a spostarsi. Per semplicità, si ipotizza di conoscere la superficie di riferimento, la velocità dell’oggetto e il coefficiente di resistenza, ma perché è importante la densità del fluido?

La densità è indice di quanto le particelle di un mezzo (fluido o solido) sono vicine tra loro.

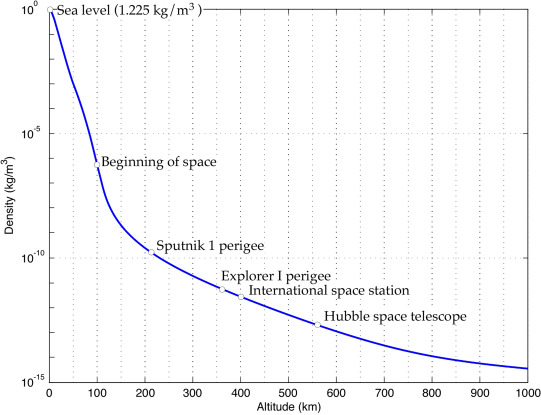
Come si evince dalla precedente figura, la densità dell’aria tende a diminuire all’aumentare della quota, pertanto più il missile incrementa di altitudine, più la densità è piccola. Ad esempio, al livello del mare si ha 1.225 $kg/m^3$ (sul grafico $10^0$, è approssimato), mentre già a quote superiore di 100 $km$ si ha un valore di circa $10^{-6}$ $kg/m^3$ (molti piccolo). Ne consegue che il suo valore influenza enormemente il valore di $D$, rendendolo abbastanza piccolo da poterlo trascurare. Ma questo è valido solo per quote elevate (es. $> 100 km$).

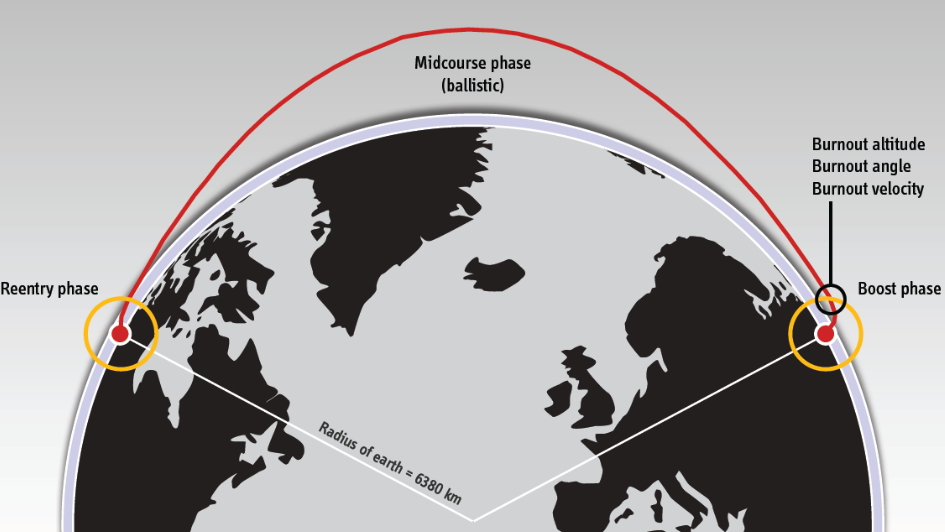
Questo aspetto è molto importante poiché, come si può facilmente evincere dall’immagine successiva

il missile balistico trascorre gran parte del tempo nella Midcourse Phase: del resto se si dovesse vincere una resistenza atmosferica elevata per tutto il tragitto, il motore non potrebbe essere spento. L’analogia con un veicolo terrestre spiega bene questo concetto: nel momento in cui togliamo il piede dall’acceleratore, l’attrito tra ruote e asfalto porta il veicolo a diminuire la sua velocità (accelerazione negativa o decelerazione) fino a fermarci. Se però si eliminasse l’asfalto o si guidasse su una lastra con un attrito molto piccolo, la macchina manterrebbe una velocità costante. Alla stessa maniera, un missile balistico mantiene, approssimativamente, la stessa velocità per un lungo periodo o, comunque, la variazione di velocità non è così elevata. 

Relativamente al raggio d’azione (range), si possono trovare numerose categorizzazioni dei missili balistici ma generalmente possono rientrare in queste categorie:

• Short range (< 1000 km)
• Medium range (1000-3000 km)
• Intermediate range (3000-5500 km)
• ICBM (>5500 km)

Inoltre i missili balistici possono rientrare nella categoria land-based, air-launched (ALBM) e submarine-launched (SLBM) ma nell’attuale articolo non si analizzeranno le varie tipologie, essendo la trattazione generica.

Il range è una caratteristica fondamentale per un missile balistico ed è spesso il criterio principale per il paragone tra i vari missili. Il range, però, non è una caratteristica intrinseca del missile stesso poiché è dipendente dal payload (carico pagante, quindi ciò che non è né struttura né propellente). Ad esempio:

• SLBM Trident, con 8 testate (dal peso di 1500 kg) presenta un range di 7500 km
• SLBM Trident, con 4 testate (dal peso di 750 kg), presenta un range di 11000 km

pertanto, ipotizzando di poter aumentare o diminuire il carico di un missile balistico a nostro piacimento, il range può variare enormemente.

Ma da cosa altro dipende il range di un missile balistico?

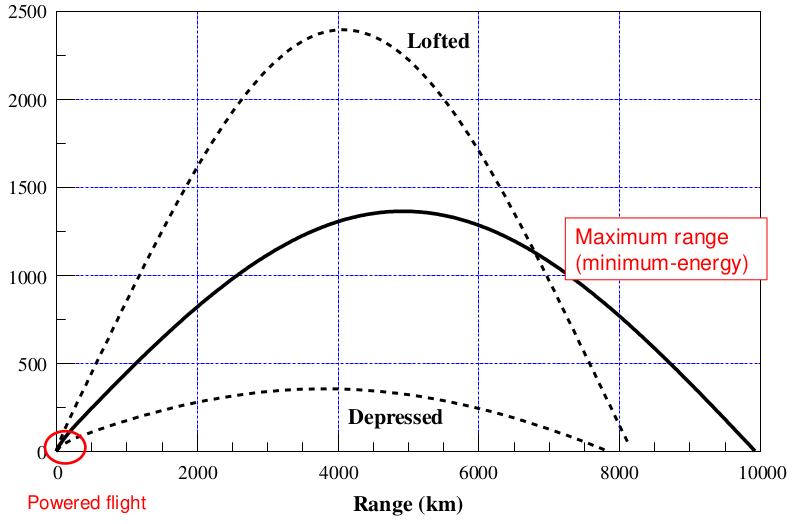
Dall’immagine precedente si comprende che, a seguito del lancio del missile, esiste un angolo che ne decreta un range più o meno elevato; tale angolo prende il nome di angolo di burn out, ovvero l’angolo che presenta il missile nel momento dello spegnimento del motore. L’angolo di burn out risulta essere l’angolo di ottimo tra gli infiniti angoli possibili.

Se si considera un missile balistico della categoria Short Range, quindi di un missile con un raggio d’azione di alcune centinaia di km, può essere ipotizzato che la curvatura terrestre non sia influente (è trascurabile, così come si era detto per la resistenza atmosferica per quota elevate). Questo permette di definire un angolo di burn-out di 45° (non a caso è lo stesso utilizzato per l’artiglieria).

Ma come si fa a scegliere l’angolo di burn out?

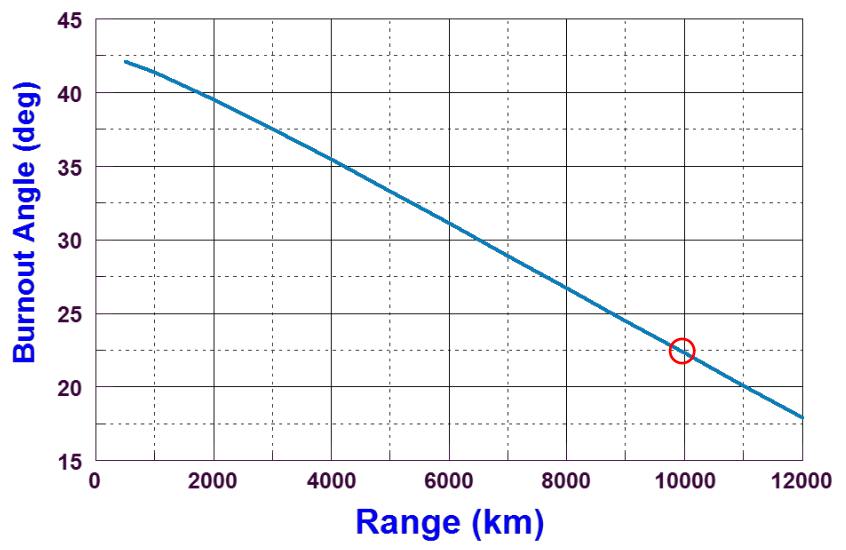
Nella progettazione di un missile, il range risulterà essere un requisito di progetto, pertanto è stabilito fin dalle fasi iniziali. Conoscendo quale deve essere il raggio d’azione del missile, tramite la precedente figura è possibile stabilire tale angolo. Ad esempio per un ICBM (>5500 km), il tipico angolo di burn out è di 22,5°. Si nota chiaramente come l’angolo di burn out tende a diminuire all’aumentare del range.

Finora si è parlato di range in relazione all’angolo di burn out ma cosa si può dire della velocità del missile?

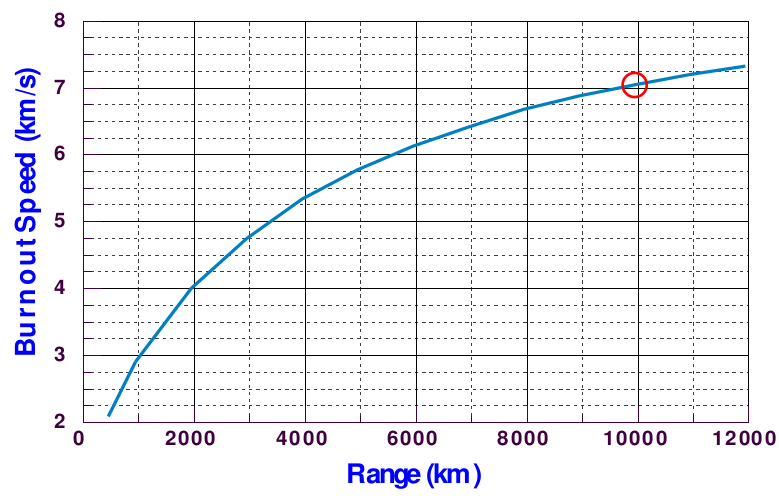
In realtà, anche la velocità di burn out, ossia la velocità che il missile presenta nell’istante in cui il motore viene spento, è molto importante. Si può graficare la velocità in funzione del range:

Avendo quindi stabilito quale deve essere l’angolo di burn out in base al range desiderato, bisogna imporre la velocità corretta in tale istante. Ad esempio, un missile SCUD che rientra nella categoria Short Range, presenta una velocità molto bassa (<2 km/s), mentre un ICBM necessita di una velocità di circa 7 km/s. Tale velocità è tipica degli oggetti che orbitano attorno alla Terra: un satellite a 300 km di quota, ha una velocità di 7.7 km/s, che tende a quella di fuga. Questo fa comprendere che tutti i Paesi che possegono vettori spaziali hanno la tecnologia necessaria per lo sviluppo di missili a lungo raggio.

Propulsione

Sebbene lo sviluppo dei missili balistici sia progredito notevolmente (a partire dal V-1), il principio di funzionamento rimane lo stesso: due serbatoi, uno contenente il propellente, l’altro l’ossidante, vengono pompati in una camera di combustione. L’unione di questi due elementi provoca una reazione che genera, fisicamente, una spinta tramite espulsione dei gas ad alta temperatura e velocità.

Dall’equazione di bilancio della quantità di moto (per i lettori non avvezzi a tale nome, è un altro modo per dire la 2° Equazione di Newton) si ha

$$\frac{d\overline{q}}{dt} = \overline{F} $$

Probabilmente il lettore si sarebbe aspettato un’altra equazione, ovvero

$$m \overline{a} = \overline{F} $$

Il problema è che quest’ultima “salta” un passaggio o, meglio, dà per scontato che la massa $m$ sia costante. Per un missile (o un razzo) non è assolutamente così. Ripartendo dalla prima, si svolgono alcuni passaggi: ricordando che la quantità di moto $\overline{q}=m\overline{v}$ allora

$$\frac{d m \overline{v}}{dt} = \overline{F}$$

$$m \frac{d\overline{v}}{dt} + \overline{v} \frac{d m}{dt} = \overline{F}$$

A questo punto si fa un’ipotesi, ovvero di trascurare le forze aerodinamiche e la forza gravitazionale, si giunge a:

$$m \frac{d\overline{v}}{dt} + \overline{v} \frac{d m}{dt} = \overline{0}$$

che riscritta in un altro modo

$$ \overline{v} \frac{d m}{dt} = -m \frac{d\overline{v}}{dt}  = \overline{T}$$

dove con $\overline{T}$ si identifica la spinta mentre si rinomina $\overline{v}$ in $\overline{v}_E$.

$$ \overline{v_E} \frac{d m}{dt} = -m \frac{d\overline{v}}{dt}  = \overline{T}$$

che si può riscrivere più facilmente come:

$$ \overline{v_E} \frac{d m}{dt}  = \overline{T}$$

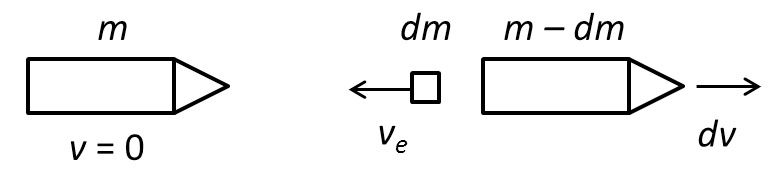
La precedente equazione la si può intendere così: come fa il missile ad accelerare? L’idea è che si parte da una massa $m$, da cui si stacca una piccola massa $dm$ (la $d$ non è una semplice lettera ma potete interpretarla come la variazione di una certa quantità, in questo caso della massa). La piccola massa $dm$ è rilasciata ad alta velocità $\overline{v}_E$, a cui corrisponde una variazione della velocità del missile, $d\overline{v}$. Insomma, ad una piccola perdita in termini di massa rilasciata ad alta velocità, corrisponde una variazione di massa e velocità del missile.

Ora che si è compreso il significato dell’equazione, si riprende un termine presente al primo membro:

$$\frac{d m}{dt} $$

Questo, che matematicamente è rappresentato da una derivata, può essere pensato comunque come un rapporto tra una massa $m$ e un tempo $t$. I lettori che si interessano di macchine o motori avranno riconosciuto già la grandezza di cui il termine è rappresentativo, ovvero la portata (portata massica, per esattezza). Per una maggior comprensione di questo rapporto, si consideri che la sua unità di misura nel Sistema Internazionale è il $kg/s$, pertanto questo termine dà informazione su quanta massa di materia transita nell’unità di tempo. 

Si hanno ora tutte le nozioni necessarie: se è valida questa equazione

$$ \overline{v_E} \frac{d m}{dt} = \overline{T}$$

allora significa che, se si vuole aumentare la spinta $T$, basterà aumentare la portata massica o tramite la velocità di uscita dall’ugello.

Relativamente alla portata massica, questa può essere modificata tramite sistemi di pompaggio ma è definita essenzialmente dalla grandezza del motore (inoltre si sta implicitamente affermando di considerare solo propellenti fluidi).

D’altra parte, la velocità dell’ugello è definita dal tipo di propellente; in generale essa si attestra tra i 2-3 $km/s$.

Si è quindi compreso che è possibile migliorare la spinta $T$ del missile tramite aumento di portata e velocità ma il limite risulta tecnologico. Una via è quindi aumentare la portata massica (magari mantenendo la stessa velocità di ugello) ma un’altra logica è invece quella di aumentare la quantità di propellente; ci si imbatterà però in un problema.

Si riparte dall’equazione di bilancio della quanaità di moto, ma la si riscrive in un altro modo:

$$ \overline{v_E} \frac{d m}{dt} = -m \frac{d\overline{v}}{dt}$$

dove possiamo pensare di moltiplicare entrambi i membri per $dt$, quindi:

$$\overline{v_E} dm = -m d \overline{v} $$

e la si riscrive in quest’altra maniera:

$$d\overline{v} = – \overline{v_E} \frac{dm}{m}$$

Operando l’integrazione:

$$\int_{\overline{v}_i}^{\overline{v}_f}d\overline{v} = – \overline{v_E} \int_{m_i}^{m_f} \frac{dm}{m}$$

dove $\overline{v}_i$ e $\overline{v}_f$ sono rispettivamente la velocità iniziale e finale del missile (chiaramente per iniziale si può considerare una qualsiasi condizione del missile, già in volo), con $m_i$ ed $m_f$ massa iniziale e finale. Riscrivendola in maniera differente, si ottiene la famosa equazione del razzo di Tsiolkovsky:

$$\Delta \overline{v} = \overline{v}_E ln(\frac{m_i}{m_f})$$

dove dietro al $\Delta$ c’è la differenza tra le precedenti velocità (finale meno iniziale).

Per semplicità nella trattazione, si ignora la massa del payload e gli effetti legati alla forza gravitazionale, quindi si riscrive l’equazione in questa maniera:

$$\Delta \overline{v} = \overline{v}_E ln(\frac{m_i}{m_f}) = \overline{v}_E ln(\frac{m_s + m_p}{m_s}) = \overline{v}_E ln(1 + \frac{m_p}{m_s}) $$

Questo ultimo passaggio è fondamentale: ipotizzando di aver definito con $m_i$ la massa iniziale del missile alla partenza mentre con $m_f$ la massa nel momento in cui il propellente è stato completamente bruciato, la differenza tra queste due masse non può essere la massa della struttura $m_s$. Con l’ultimo passaggio si evidenzia come la variazione di velocità del missile dipende dal rapporto massa del propellente su massa della struttura (ovviamente si può parlare anche dell’inverso).

Quindi, se l’obiettivo risulta essere di aumentare la velocità del missile, si potrebbe aggiungere il propellente, ma per aggiungere il propellente si ha sicuramente bisogno di più spazio, quindi di una struttura più grande; questo significa che con l’aumentare del propellente aumenta anche la massa della struttura. Questo fa comprendere che, volendo far in modo che il rapporto tra $m_p$ ed $m_s$ sia sempre più grande non è poi così semplice ottenerlo, poiché i due termini sono legati intimamente.

Non è un caso che i moderni lanciatori spaziali hanno (circa) 90% di propellente, meno del 10% di struttura e quel che rimane il payload.

Per completezza della trattazione, si ricorda che parte fondamentale nella progettazione di un missile ricade nel Guidance, Navigation and Control (GNC): tale settore è indirizzato allo studio e alla progettazione dei sistemi di controllo atti a controllare il missile durante il suo moto. Tra questi c’è anche il controllo della spinta; in particolare, è questo sistema che disattiva il motore quando necessario o che effettua le operazioni di rientro della testata.

Il controllo della spinta è oggi dedicato da sistemi molto complessi, definiti TVC (Thrust Vectoring Control), che permettono di direzionare l’ugello propulsivo laddovè è necessario. In precedenza molti missili balistici (es. SCUD) presentavano degli jet vanes, la cui rotazione decretava il re-direzionamento della spinta. Lo svantaggio di tale sistema è che si va ad influenzare il flusso dei gas uscenti, provocando una diminuzione della spinta.

Rientro ed Accuratezza

La fase di rientro della testata (convenzionale o nucleare) del missile balistico risulta essere la fase decisiva e, al tempo stesso, più difficile nella progettazione. Le velocità, forze e sollecitazioni termiche che agiscono sugli oggetti in rientro nell’atmosfera terrestre sono elevatissimi. Relativamente alle sollecitazioni termiche, ogni oggetto (aeromobile o missile) che voli, subisce degli stress termici continui, dal momento che la resistenza dell’aria provoca un aumento della temperatura su tutta la superficie del corpo. Normalmente sugli aeromobili si hanno temperature molto elevate (centinaia di °), anche a velocità modeste. Se quindi si pensa ad una testata di un missile balistico in rientro nell’atmosfera, la resistenza atmosferica, non più trascurabile, tende a rallentarla, generando così non solo elevate forze sulla struttura ma anche alte temperature.

L’obiettivo, però, è quello di riuscire a mantenere (idealmente) la stessa velocità in rientro dall’atmosfera, altrimenti la testata risulterebbe più facilmente intercettabile.

Per farlo è necessario introdurre un ultimo concetto, quello di weight-to-drag ratio o più comunemente noto come coefficiente balistico (ballistic coefficient)

$$\beta = \frac{mg}{C_D A}$$

dove $m$ è la massa della testata, $g$ è l’accelerazione di gravità, $C_D$ è il coefficiente di resistenza della testata mentre $A$ è superficie di sezione. Si definisce weight-to-drag ratio poiché è il rapporto tra un peso ed una resistenza (formalmente, però, il rapporto ha le dimensioni di una pressione $Pa$, $N/m^2$), $lb/ft^2$, ecc.). 

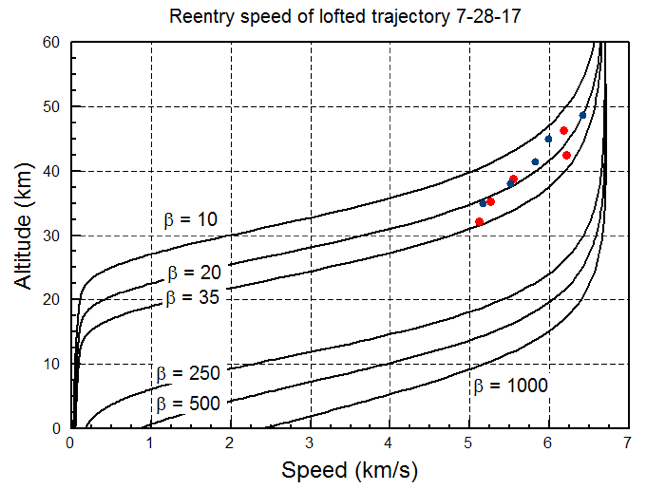
Dal precedente grafico si può fare la seguente osservazione: il coefficiente balistico $\beta$ influisce enormemente sul valore della velocità a quota $0$, in particolare più è grande tale valore tanto più la velocità tenderà a mantenersi vicina a quella di rientro, perlomeno fino a poche decine di $km$ dove la variazione di velocità tende a farsi sentire. È però preferibile avere un $\beta$ grande dal momento che la variazione di velocità, sebbene sia sempre presente, porti la testata ad impattare a velocità elevate, mentre per valori di $\beta$ piccoli, il decremento di velocità avviene a quota maggiore e tende a (circa) 0 $km/s$ già a molte decine di $km$ di quota. In tal caso, la testata sarebbe facilmente intercettabile dai moderni sistemi anti missile.

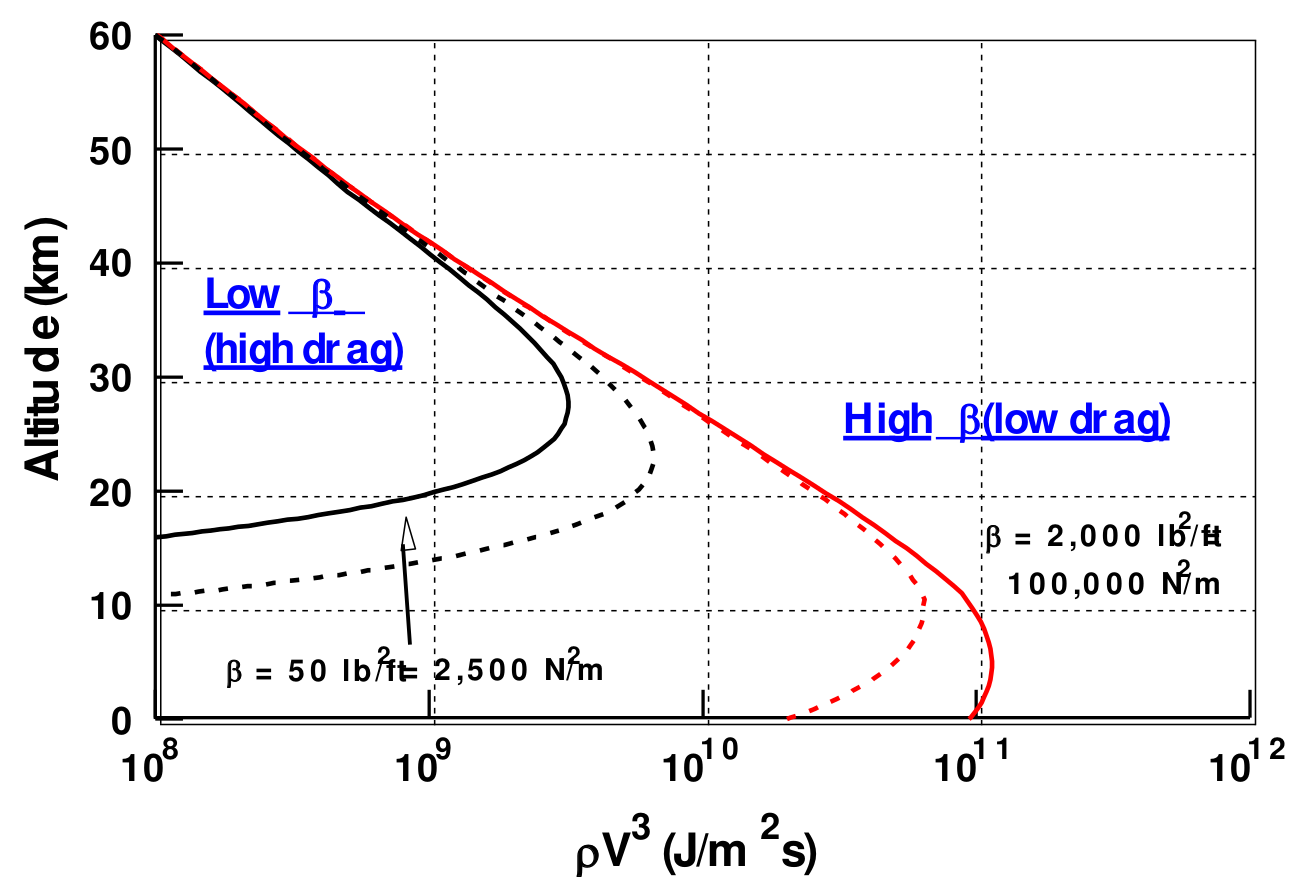
Si è compreso che è preferibile un $\beta$ elevato, ma questo ha uno svantaggio.

Il precedente grafico mostra che valori differenti di $\beta$ non influenzano solo la velocità di impatto della testata ma anche il trasferimento di calore sul sistema. Sulle ascisse si ha, infatti, $\rho V^3$, grandezza legata allo scambio termico, mentre sulle ordinate la quota, come nel precedente grafico. Scegliendo quindi un $\beta$ grande per ciò che è stato detto in precedenza, si va incontro inevitabilmente a valore molto più elevato di $\rho V^3$ (quindi calore più inteso, che dovrà essere sopportato dalla struttura). Ovviamente a valori elevati di $\beta$ corrisponde anche una resistenza atmosferica più piccola (sarò chiaro nell’ultima figura) dal momento che, riprendendo la formula di $\beta$

$$ \beta = \frac{mg}{C_D A} $$

un $\beta$ grande significa avere il denominatore piccolo (l’area $A$ è fissata, quindi è il coefficiente di resistenza piccolo). E’ sicuramente un vantaggio dal punto di visto aerodinamico e che porta a mantenere un valore di energia cinetica maggiore (come visto in precedenza). Dall’altra parte, invece, un $\beta$ piccolo significa avere uno scambio termico più contenuto, preferibile se l’oggetto in questione è, ad esempio, una capsula.

Non è infatti un caso che le capsule di rientro hanno una forma che ricorda un fungo ($\beta$ piccolo) mentre le testate nucleari di un ICBM Minuteman III hanno una forma conica ($\beta$ elevato).

 

Fonte: armscontrolwonk.com