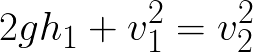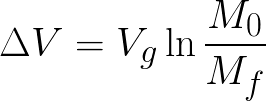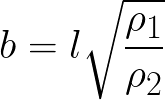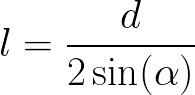Per bomba anti-bunker (bunker-buster bomb) si intende un ordigno in grado di penetrare all’interno di un obiettivo grazie all’energia cinetica associata e tramite cariche esplosive che “scavano” un canale verso il target.
Il fatto che si parli di bomba non deve far confondere il lettore: sono stati progettati missili, cruise e bombe per effettuare operazioni con tale scopo. Il vettore quindi può essere generico ma le caratteristiche al fine delle penetrazione sono le stesse.
Nei conflitti moderni moltissime installazioni militari sono posizionate nel sottosuolo (per esempio le infrastrutture di arricchimento dell’uranio in Iran oppure i tunnel scavati in Siria), pertanto è sempre più richiesta la capacità di poter infliggere danni a tali strutture in quanto costruite spesso a decine di metri di profondità.
Tali strutture sono definite con l’acronimo HDBT (Hard and Deeply Buried Target) e indicano tutte quelle costruzioni più o meno complesse che non sono solo protette dal suolo ma anche da elementi strutturali, edificati con lo scopo di rinforzare l’intero edificio.
In realtà la sfida di riuscire a distruggere infrastrutture critiche sotterranee riguardò tutto il periodo della Guerra Fredda ma fu risolto con le RNEP (Robust Nuclear Earth Penetrator): si tratta di ordigni nucleari che, una volta penetrati nel suolo per via dell’energia cinetica del vettore, esplodono generando quindi una reazione nucleare. Tale tattica ovviamente è stata abbandonata con gli anni per via delle conseguenze di tali esplosioni ed è ovviamente frutto del suo periodo storico.
Tra i più noti bunker-buster troviamo:
| Sistema d’arma | Penetrazione | Kit di guida |
| BLU-109 | 1,8 m di calcestruzzo | GBU-10, GBU-15, GBU-24, GBU-27, AGM-130 |
| BLU-116 | 3,4 m di calcestruzzo rinforzato | GBU-15, GBU-24, GBU-27, AGM-130 |
| BLU-118/B | 3,4 m di calcestruzzo rinforzato | GBU-15, GBU-24, AGM-130 |
| BLU-113 | >6 m di calcestruzzo rinforzato | GBU-28, GBU-37 |
| Big BLU o MOP | 61 m di calcestruzzo rinforzato (non ancora verificato) | GBU-57A/B |
I sistemi d’arma vanno intesi come modelli standard dell’ordigno in questione a cui si possono aggiungere dei kit per la guida (esempio GBU sta per Guided Bomb Unit). La Big BLU risulta l’ultimo sistema d’arma (noto) sviluppato, con peso di 13 t.
I prossimi anni vedranno lo sviluppo di un penetratore ad alta velocità (con velocità di impatto maggiori di 1200 m/s) con peso di circa 1 t contro le >2 t degli attuali bunker-buster ma con la stessa capacità di poter distruggere calcestruzzo rinforzato (avente massima resistenza meccanica di compressione tra 4,9÷36 MPa). Il vettore dovrà inoltre avere una dimensione ridotta per poter essere lanciato dagli F-35 o futuri velivoli.
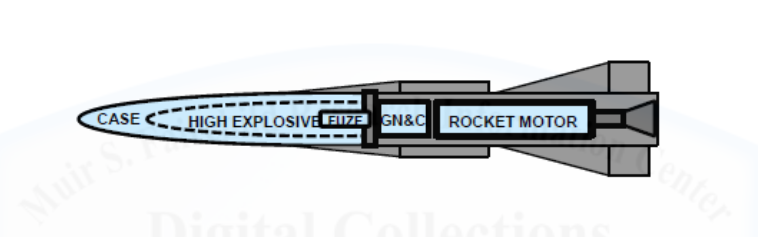
La capacità di sopravvivenza di tale sistema d’arma dipenderà dal peso, dall’angolo e dalla velocità di impatto e dai materiali utilizzati.
Meccanica di penetrazione della bomba anti-bunker
I sistemi d’arma sviluppati per la distruzioni di HDBT si basano principalmente sull’energia cinetica dell’intero vettore e, in alcuni casi, anche da una (o più) cariche cave presenti all’interno del sistema. Per carica cava si intende una carica esplosiva che presenta una cavità con una precisa geometria (in genere conica) e che, una volta detonato l’esplosivo, si deforma generando un getto ad alta velocità lungo l’asse centrale.
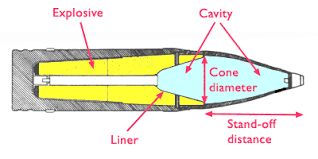
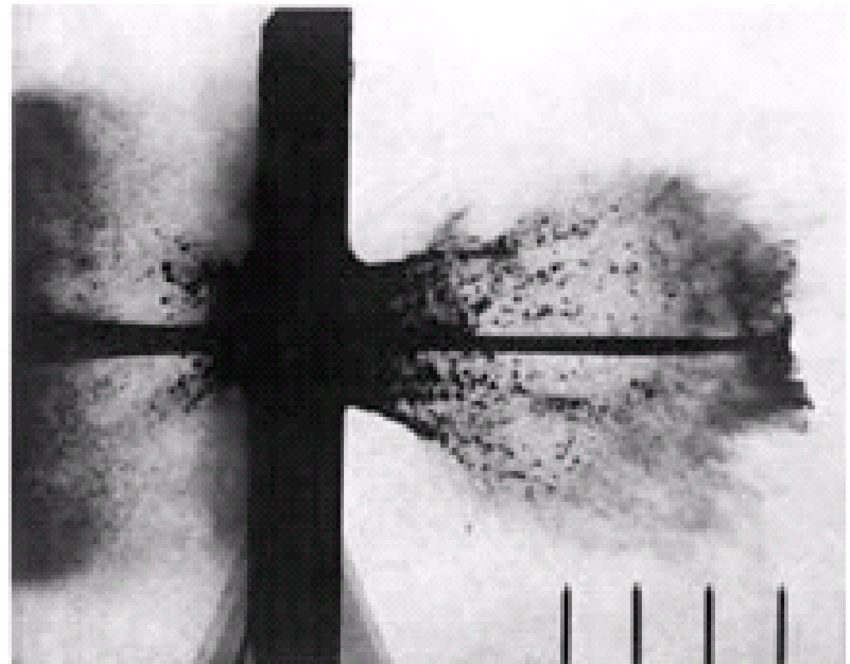
Contrariamente a ciò che si può pensare, il getto ad alta velocità non perfora per via dell’alta temperatura (non raggiunge necessariamente il punto di fusione dei materiali) ma è l’elevatissima pressione generata che deforma obiettivi con dimensioni di 7÷10 volte il diametro della carica. Le velocità in questione sono elevatissime: la punta del getto viaggia tra 7 e 14 km/s mentre la coda tra 1 e 3 km/s.
Con tali caratteristiche, il processo di penetrazione genera pressioni cosi elevate che possiamo approssimare il getto come un fluido incomprimibile, in grado di ignorare completamente la resistenza meccanica dell’obiettivo.
Anche se lo sviluppo di tale detonazione è brevissimo, le particelle che costituiscono il getto tendono nel tempo ad allontanarsi dall’asse centrale, riducendo così la capacità penetrativa della carica cava.
Ovviamente lo stesso vettore dovrà essere costituito da un materiale ad elevata resistenza meccanica in modo tale da sopportare la pressione che si genera sull’obiettivo. Gli ordigni hanno spesso strutture costruite in tugsteno o altri materiali performanti.
Modello Fisico di un EPW (Earth Penetrating Warhead)
Si riporta di seguito un modello fisico della penetrazione di un ordigno. Si analizzano gli aspetti legati alla velocità di impatto, alla profondità di penetrazione per via dell’energia cinetica e tramite la carica cava.
Per modello fisico si intende una rappresentazione del fenomeno in analisi in cui si sono state considerate delle ipotesi e dove sono state utilizzate delle approssimazioni. Ipotesi e approssimazioni sono necessarie per semplificare lo studio ma il risultato dell’analisi rimane valido in quanto vicino alla realtà.
Ipotesi iniziali:
- L’impatto dell’ordigno con il terreno avviene perpendicolarmente (bomba cade in verticale sulla terra che è perfettamente orizzontale)
- Ordigno considerato come corpo rigido: la resistenza meccanica dell’obiettivo, che corrisponde dimensionalmente ad una pressione, comporta una uguale distribuzione della decelerazione (accelerazione negativa) di tutti i punti dell’ordigno.
Per corpo rigido si intende una distribuzione continua di punti materiali nello spazio a cui si impone il vincolo della rigidità: significa che presi due qualunque punti del corpo rigido, la distanza tra i due punti rimane costante nel tempo, a prescindere dalle eventuali sollecitazioni (esempio la pressione esercitata dal terreno sull’ordigno).
In sintesi le affermazioni di sopra indicano che l’angolo di impatto non è generico e il vettore è da considerarsi come indeformabile.
Caduta e Penetrazione nell’obiettivo
Si introducono nella spiegazione alcuni concetti della meccanica classica necessari alla comprensione delle equazioni riportate nel seguito.
Un ordigno rilasciato da un’altezza h da un velivolo o che scende in picchiata dopo un volo di crociera presenta all’impatto con il terreno una certa velocità. La velocità di impatto è importantissima per la capacità di penetrazione in un obiettivo.
Per calcolare tale velocità si introduce l’energia meccanica, somma di energia cinetica K e potenziale U: l’energia meccanica è quindi legata alla posizione e alla velocità di tale oggetto.
Considerando due istanti di tempo differenti, l’energia meccanica si conserva (non stiamo considerando fenomeni di attrito), pertanto il primo membro dell’equazione riportata di seguito deve essere uguale al secondo membro (nell’istante 1 avremo una certa energia cinetica e potenziale, la cui somma è uguale anche all’istante 2 ma i singoli termini possono avere valori differenti, per esempio 1+3=2+2).
Poiché il nostro oggetto si trova soggetto ad un campo gravitazionale, la sua energia potenziale dipende unicamente dall’altezza, calcolata rispetto un sistema di riferimento (esempio il terreno). Quindi trascurando eventuali forze dissipative (per esempio l’attrito con l’aria), possiamo scrivere:
Esplicitando i termini:
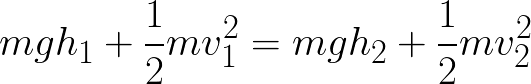Nell’equazione precedente v1 rappresenta la velocità iniziale dell’ordigno e h1 la sua altezza iniziale (si ipotizza per esempio che la bomba sia posizionata come nell’immagine seguente). Una volta avvenuto l’impatto con il suolo, la sua altezza sarà h2 ma è un valore nullo in quanto l’origine del riferimento è proprio il terreno, mentre la velocità di impatto è v2. La massa è definita con m mentre l’accelerazione di gravità con g.
Si rammenta che il peso di un oggetto non è pari alla sua massa. La massa indica la quantità di materia presente in un corpo, mentre il peso è la forza pari alla massa moltiplicata per l’accelerazione di gravità (si parla infatti di forza peso):
Si calcola quindi la velocità di impatto della bomba:
L’altezza dell’ordigno nel momento in cui tocca il suolo è:
Si semplifica l’equazione dell’energia meccanica in:
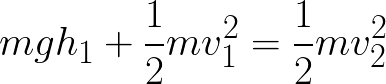Si effettuano delle semplificazioni considerando la massa dell’ordigno costante durante la discesa (è una semplificazione in quanto potremmo considerare missili che utilizzano il carburante rimanente per la spinta nella fase finale).
Che diventa:
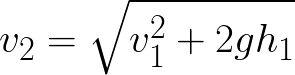Per esempio con un’altezza h1 = 10.000 m, g = 9,81 m/s² e v1 = 0 m/s (caso di caduta libera) si ha una v2 = 450 m/s.
In alcuni casi i vettori (missili o cruise) potrebbero presentare dei propulsori che portano un incremento della velocità di impatto; nella fase finale è possibile utilizzare il combustibile per aumentare la velocità di impatto.
Per il calcolo dell’incremento della velocità da sommare alla v2, si utilizza la seguente relazione:
Dove:
- ΔV è l’incremento di velocità [L/T]
- Vg è la velocità dei gas in uscita dal propulsore [L/T]
- M0 è la massa iniziale del vettore [M]
- Mf è la massa finale del vettore [M]
Per esempio se consideriamo Vg = 2500 m/s (combustibile liquido) e che il vettore utilizza solo l’1% della sua massa per la propulsione (quindi il rapporto tra massa iniziale e finale è 1/0.99) si ha un incremento ΔV di 25 m/s.
Pertanto la velocità di impatto è:
A questo punto si passa all’analisi della profondità della penetrazione di una bomba e per farlo si introducono alcuni concetti fondamentali.
Per il principio di azione e reazione (3° Legge di Netwon) un corpo 1 che esercita una forza F su un corpo 2, subirà una forza uguale e opposta, quindi esercitata dal corpo 2 al corpo 1.
Tale principio deve essere applicato al caso in analisi: la bomba (corpo 1) esercita una forza F sul terreno (corpo 2) ma quest’ultimo si opporrà all’ordigno con la stessa intensità ma verso opposto.
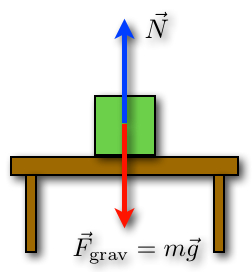
Quando si ha una forza F che agisce su una certa area A (per esempio la scatola verde che esercita il suo peso su un’area del tavolo) si deve allora parlare di pressione P: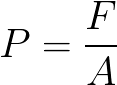
Tornando all’analisi del fenomeno, nel momento in cui l’ordigno impatta sull’obiettivo, esso esercita un certo carico (inteso come pressione) che è proporzionale in parte al suo peso e a tutte le forze che fino al momento prima dell’impatto stavano agendo su di esso (forze aerodinamiche, forze dovute ad eventuali sistemi di propulsione, ecc).
Per il terzo principio della dinamica, il terreno (o un eventuale altro mezzo) esercita sull’interfaccia bomba-terreno una pressione uguale che, per la seconda ipotesi fatta, comporterà una decelerazione uniforme su tutto il corpo.
La pressione esercitata dal terreno sull’ordigno è la resistenza meccanica; se quindi la struttura è in grado di sopportare tale pressione allora riuscirà ad avanzare nell’obiettivo (per la stessa ipotesi il corpo è indeformabile).
La bomba avanzerà, senza deformarsi, fintanto che la sua velocità non si annullerà per via di una decelerazione progressiva della bomba a causa della pressione del mezzo in cui transita (sappiamo che ciò non è vero ma il modello fisico è una semplificazione).
La teoria di penetrazione di un proietto all’interno di un mezzo è molto complessa e ci sono molti metodi di calcolo (che portano anche a risultati differenti in base alle variabili in gioco).
Nella teoria presentata si considera una relazione semplice che lega la profondità della penetrazione con energia cinetica, resistenza meccanica del materiale e la massima area trasversale della bomba (approssimativamente è come guardare l’ordigno dall’alto e considerare la sua area massima).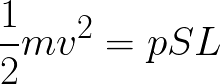
Dove:
- m è la massa della bomba [M]
- v è la velocità di impatto della bomba [L/T²]
- p è la pressione esercitata dal mezzo (es. il terreno) sulla struttura dell’ordigno, quindi è la resistenza meccanica [F/L²]
- S è la massima sezione della bomba [L²]
- L è la nostra incognita ossia la distanza di penetrazione [L]
(Sono state riportate le dimensioni tra le parentesi quadrate per chi volesse effettuare l’analisi dimensionale)
La velocità di impatto è stata trovata prima, la massa dell’ordigno la conosciamo, la sezione S è nota quindi manca solo la resistenza meccanica p. Tale grandezza dipende dal tipo di materiale che andiamo a considerare ed è un valore empirico (quindi calcolato tramite dei test in laboratorio).
Di seguito si riporta una tabella con alcuni materiali comuni e le loro proprietà meccaniche principali (i valori riportati sono stati estratti da una pubblicazione scientifica ma in altri testi potrebbero presentare intervalli o valori differenti).
| Materiale | Densità (kg/m³) | Resistenza meccanica (MPa) |
| Calcestruzzo rinforzato | 2000÷2200 | 4,9÷36 |
| Laterizio | 1600÷1700 | 7÷29 |
| Granito | 2010÷2250 | 147÷255 |
| Ghiaccio (Acqua in stato solido) | 900 | 1÷2 |
| Sabbia | 1200÷1600 | 0,1÷1 |
| Arenaria | 1500÷1800 | 1÷5 |
| Ghiaia | 1500÷2000 | 1÷4 |
| Corazzatura in Acciaio | 7900 | 373÷412 |
L’operatore ÷ indica un intervallo (es. tra 2 e 5 si scrive 2÷5)
Scelto il materiale, possiamo calcolare la profondità L utilizzando l’equazione precedente (si porta ad un membro il solo termine di cui siamo interessati):
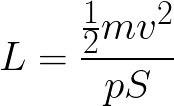Per esempio se consideriamo una massa m = 2000 kg (valore comune di una bomba), S = 0,225 m², v = 450 m/s e p = 36 MPa (calcestruzzo rinforzato) si ottiene L = 25 m.
Tale valore rientra, per intensità, in quelli riportati nella prima tabella che riguardavano i più comuni vettori anti-HDBT. Del resto gli attuali ordigni in utilizzo contro bunker raggiungono profondità che vanno da pochi metri al caso (non verificato) della Big BLU di circa 60 m.
E’ ovviamente un valore approssimativo in quanto non abbiamo tenuto conto di molti fattori.
Durante la Seconda Guerra Mondiale al posto dell’equazione vista si utilizzava la seguente:
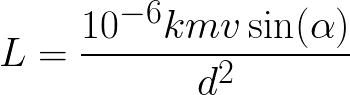usata per il calcolo della penetrazione dei proietti nei bunker, dove:
- L è la profondità della penetrazione [L]
- k è il coefficiente di penetrazione [L²T/M]
- m la massa del proietto [M]
- v la velocità del proietto [L/T]
- d il calibro dell’arma [L]
- α (alpha) è l’angolo che si forma all’impatto tra il proietto e l’obiettivo (che si ipotizza sia orizzontale come il terreno) [1]
Si riportano i coefficienti di un proiettile di artiglieria relativi alla penetrazione di un bunker:
| Materiale | Coefficiente k |
| Calcestruzzo rinforzato | 0,7÷1,3 |
| Laterizio | 3 |
| Tronchi di pino | 6 |
| Sabbia | 4,5 |
| Sabbia non compatta | 9 |
| Argilla compatta | 7 |
Si nota quindi che più è elevato il coefficiente k, più la profondità è elevata mentre se si aumenta il calibro dell’arma si ha una diminuzione della penetrazione.
Per completezza della trattazione si riporta anche una relazione approssimata per il calcolo della profondità “scavata” tramite una carica cava di forma conica:
per il calcolo di l:
Dove:
- b è la profondità raggiunta tramite la carica [L]
- l è la lunghezza del getto [L]
- ρ1 (rho) è la densità del rivestimento della carica [M/L³]
- ρ2 (rho) è la densità del mezzo in cui avviene l’esplosione [M/L³]
- d è il diametro della carica cava [L]
- α (alpha) è l’angolo che si forma tra la verticale e l’asse del vettore [1]
In conclusione, un vettore che presenta una carica cava (o più cariche) utilizza in buona parte la sua energia cinetica (velocità di impatto) per penetrare nel materiale dell’obiettivo, dovendo però sostenere la compressione sull’intera struttura (nella trattazione non è stato calcolata la compressione assiale sul vettore). Nel momento in cui la velocità inizia a diminuire, una o più cariche esplodono, permettendo di scavare un canale a profondità maggiori.
Con il rispetto delle ipotesi di partenza, le equazioni riportate vi permettono di:
- calcolare la profondità massima raggiunta con la sola energia, cinetica considerando il vettore come corpo rigido ed escludendo forze di attrito nella caduta
- calcolare la profondità scavata da una carica cava di forma conica
Fonti:
https://it.wikipedia.org/wiki/Robust_Nuclear_Earth_Penetrator
DEFEATING HARD AND DEEPLY BURIED TARGETS IN 2035 by Russell J. Hart, Jr., Colonel, USAF
New Self-Propelled Penetration Bomb, Alexander Bolonkin, Shmuel Neumann
